Answers: Correlation and simple linear regression
Homework 9: Correlation and simple linear regression
Answers to selected number problems
Answers to selected problems
Part 1
1.
install.packages("MASS")
library(MASS)
data(Animals, package="MASS")
classType <- c("M","M","M","M","M","D","M","M","M","M","M","M","M","H","M","D","M","M","M","M","M","M","M","M","M","M","D","M")
dAnimals <-data.frame(classType,Animals)
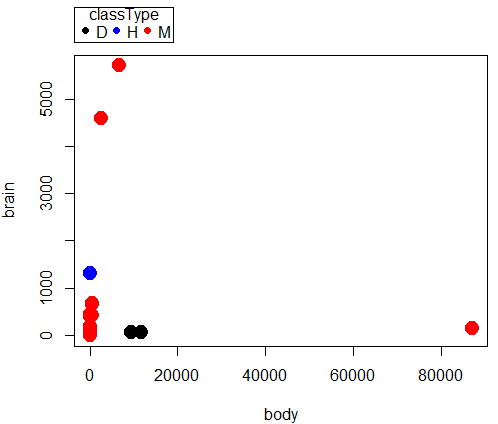
scatterplot(brain~body | classType, regLine=FALSE, smooth=FALSE, by.groups=TRUE, pch=c(19,19,19), cex=c(2,2,2), col=c("black", "blue", "red"), grid=FALSE, data=dAnimals)
a)
3. normalityTest(~brain, test="shapiro.test", data=Animals) Shapiro-Wilk normality test data: brain W = 0.45173, p-value = 0.000000003763
Clearly, we reject null hypothesis, “brain” not normally distributed.
normalityTest(~body, test="shapiro.test", data=Animals) Shapiro-Wilk normality test data: body W = 0.27831, p-value = 1.115e-10
Clearly, we reject null hypothesis, “body” not normally distributed.
5.
Rcmdr: Statistics → Summaries → Correlation test
with(Animals, cor.test(body, brain, alternative="two.sided", + method="spearman")) Spearman's rank correlation rho data: body and brain S = 1036.6, p-value = 0.00001813 alternative hypothesis: true rho is not equal to 0 sample estimates: rho 0.7162994
Question 1. Parametric tests involve estimation of population parameters, e.g., correlation between body weight of “mammals” and brain weight of “mammals”. Parametric statistics require certain assumptions hold, for example, normality. Nonparametric tests test similar hypotheses, but do so on ranks, not the original data. Thus, fewer assumptions are made about the quality of the data as no effort is made to infer population parameter values.
Question 3. Spearman rank correlation (0.716, P = 0.000018) is best and we conclude there is a positive association between brain and body weight in this sample of mammal species. Note that the Pearson product moment correlation was small and negative (-0.0053), and not statistically different from zero (P = 0.979). However, we can’t trust this estimate because the assumption of normality was clearly violated for both these variables (brain weight: p-value = 0.000000003763; body weight: p-value = 1.115e-10. See normality test #5 above).
Part 2
1. There are just two variables. “speed” is clearly an independent variable whereas “dist” (stopping distance) is the dependent variable.
2. scatterplot

3. histogram
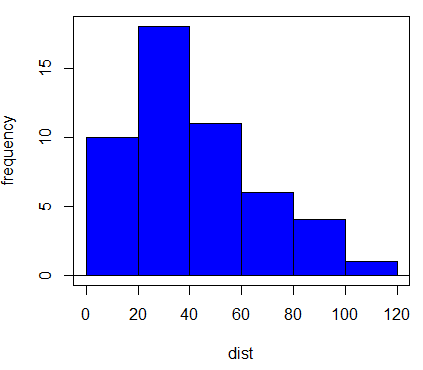
4. dist, Shapiro-wilk p-value = 0.0391
Question 1. Because we reject normality assumption for dist, we log10-transform dist to create new variable, lgDist. However, lgDist is even less normally distributed (Shapiro-Wilk normality test p-value = 0.001066), we conduct our linear regression test of speed on untransformed dist.
Results were
lm(formula = dist ~ speed, data = myData) Residuals: Min 1Q Median 3Q Max -29.069 -9.525 -2.272 9.215 43.201 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -17.5791 6.7584 -2.601 0.0123 * speed 3.9324 0.4155 9.464 1.49e-12 *** Residual standard error: 15.38 on 48 degrees of freedom Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438 F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12
Rcmdr: Models → Hypothesis tests → ANOVA table
Anova(LinearModel.3, type="II")
Anova Table (Type II tests)
Response: dist
Sum Sq Df F value Pr(>F)
speed 21186 1 89.567 1.49e-12 ***
Residuals 11354 48
6.
a) b0 (Y-intercept) = -17.5791
b) Null hypothesis: Y-intercept equals zero. P-value = 0.0123, therefore we reject null hypothesis
c) b1 (slope) = 3.9324
d) Null hypothesis: slope equals zero. P-value = 1.49e-12, therefore we reject null hypothesis
e) dist = -17.5791 + 3.9324(speed)
f) Adjusted R-squared: 0.6438
7.
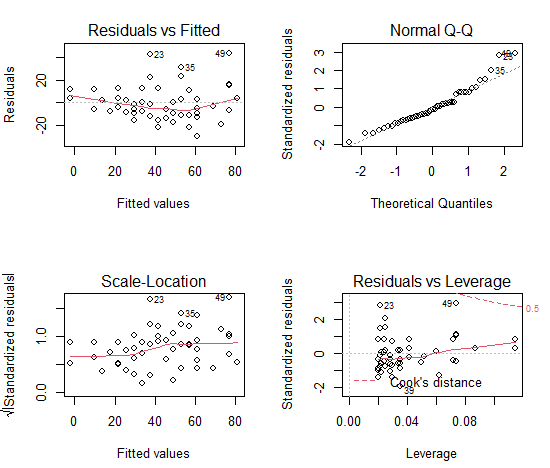
Top-left graph: No obvious trend in residuals
Top-right graph: Q-Q plot suggests some deviation from normality (points 25, 35, 49), which is consistent with our test of normality
Bottom left graph: some trend in variances; increases with increasing fitted (predicted) values
Bottom right graph: No evidence of influence point (no data outside Cook’s distance, see dashed red line)
Numerical diagnostics: Only numerical test appropriate is Breusch-Pagan test of variance of errors normally distributed (no heteroscedasticity)
Breusch-Pagan test data: dist ~ speed BP = 4.6502, df = 1, p-value = 0.03105
Question 3. We conclude that our simple model, knowing speed of the car, explains 64% of variance in stopping distance. Some indications that distance not normally distributed and a possible pattern in residuals (BP test significant for heteroscedasticity), which may warrant additional addition.