Answers: Multiway ANOVA
Answers to selected problems
1. How many variables? Which variables are the factors? How many levels in each variable/factor?
Three variables: Factor1, Factor2, Response
Clearly, two. After all, the one is labeled Factor1, the other is Factor2. But more generally, we can tell they are factors because the datatypes are categorical, nominal.
Three levels in Factor1 (G,H,I) and three levels in Factor2 (A,B,C)
2. Write out all null hypotheses that can be tested in this 2-way ANOVA problem.
H0: No difference among means Factor1
H0: No difference among means Factor2
H0: No interaction between Factor1 and Factor2
3. Write out the equation for the model.
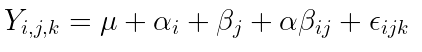
4. Crossed design. For every level in Factor1, we see levels of Factor2.
| Factor1 | Factor2 |
| G | A, B, C |
| H | A, B, C |
| I | A, B, C |
5. ANOVA are parametric tests, so assumptions are: Response variable normally distributed. Equal variances among the different groups
6. Friedman test. We haven’t discussed this, but you’ll find the answer if Mike’s Biostatistics Book
7. Rcmdr: Graphs > Plot of means
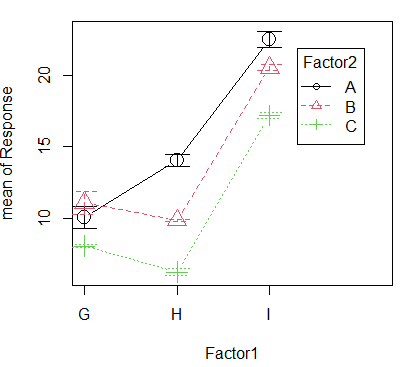
Note: The lines aren’t parallel, so we expect to see an interaction between Factor1 and Factor2.
8. Normality test
Shapiro-Wilk normality test data: Response W = 0.9169, p-value = 0.03326
9. Equal variance test
Rcmdr: Statistics > Variances > Levene’s test (select median)
I run the variance tests as one-way problems
leveneTest(Response ~ Factor1, data=ex2way, center="median") Df F value Pr(>F) group 2 1.627 0.2175 24
leveneTest(Response ~ Factor2, data=ex2way, center="median") Df F value Pr(>F) group 2 0.0542 0.9474 24
10. Conduct the ANOVA test
AnovaModel.1 <- lm(Response ~ Factor1*Factor2, data=ex2way, contrasts=list(Factor1 ="contr.Sum", Factor2 ="contr.Sum"))
Anova(AnovaModel.1) Anova Table (Type II tests) Response: Response Sum Sq Df F value Pr(>F) Factor1 616.94 2 491.803 < 2.2e-16 *** Factor2 116.76 2 93.076 0.000000000322 *** Factor1:Factor2 30.08 4 11.991 0.000063278861 *** Residuals 11.29 18
more to come…